Part B
Determining Distances & Locating Places
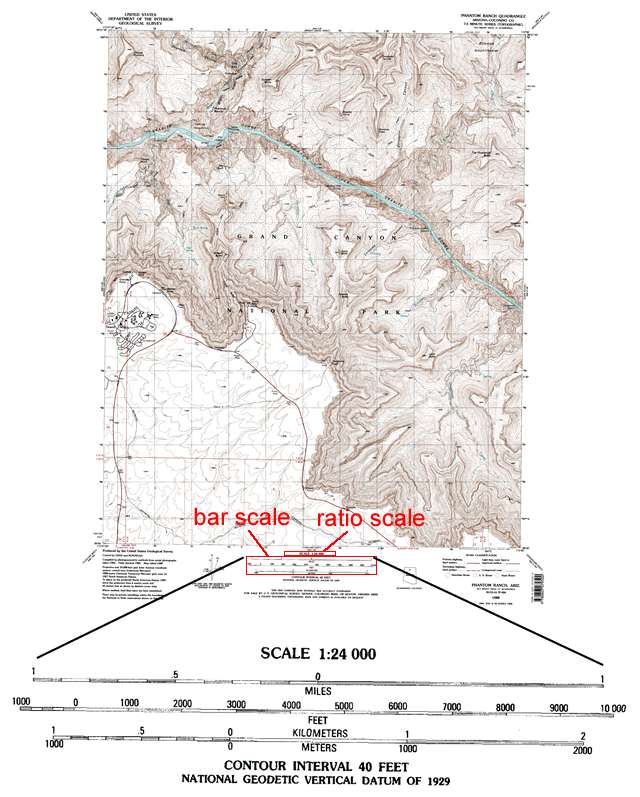
Since topographic maps and air phoros represent/show the Earth's surface, they can be used to determine distances between points. Knowing the scale of the map provides a way to determine the distance between points on the map. There are three types of scales: graphical, ratio, and vebal, two of which are typically displayed at the bottom center of a topographic map.
|
|
|
Figure 2-17. The ratio scale and graphical (bar) scales for a 7.5 minute topographic map. |
Determining Distances
Graphical Scale
A graphical scale is commonly shown as a bar scale. Most maps have three scale bars: one in miles, one in feet, and one in kilometers. Bar scales are relatively easy to use. One way to measure a distance is to just measure a distance on the map and then compare it to one of the graphical scales.
|
Example 13 |
|
How far apart (in kilometers) are Mather Point and Yaqui Point? |
|
1) Using any straightedge or ruler, mark the distance between the two points. |
|
|
|
2) Place this measurement against the kilometer bar scale and estimate the distance. |
|
It's about 2200 m or 2.2 kilometers |
![]()
![]()
Ratio Scale
A ratio scale is given numerically as a ratio (e.g., 1:24,000, 1:62,500, 100,000, etc.) and is also typically located at the bottom center of most published topo maps, just above the bar scales. In most cases, it enables a more precise measurement of distance than using graphical scales. A ratio scale is simply a comparison of map distances with actual "real world" distances. For example, 1:24,000 means that one centimeter on the map equals 24,000 actual centimeters on Earth's surface. Two centimeters on the map equal 2*24,000 centimeters or 48,000 centimeters.
|
Example 14 |
|
A map has a ratio scale of 1:62,500. |
|
1 inch on the map = 62,500 on the Earth's surface, |
![]()
![]()
Verbal Scale
The verbal scale is a comparison of map distances with actual "real world" distances. For example, a ratio scale of 1:24,000 means that one centimeter on the map equals 24,000 actual centimeters on the Earth's surface. Well, that's great, but how far is 24,000 centimeters? We need to convert 24,000 centimeters into a more usable unit.
Hint
When calculating 1 cm = ? m, divide the map scale by 100 (there are 100 cm in 1 m).
When calculating 1 cm = ? km, divide the map scale by 100,000 (there are 100,000 cm in 1 km).
To do this, we divide by 100 (there are 100 cm in one m). Thus, the verbal scale would be "one centimeter on the map = 240 meters on the Earth's surface".
For any given map, you'll only have to do this conversion once. So to calculate "real world" distances, all you have to do is measure the distances between points on the map and multiply by this conversion.
|
Example 15 |
|
On a map, points A and B are 3 centimeters apart. How many kilometers is this? |
|
1) Find the ratio scale of the map. 1:24,000 (so, 1 cm on the map = 24,000 cm on the Earth's surface) |
|
2) Convert the ratio scale 1:24,000 to a verbal scale. 1 cm on the map = 24,000 cm "on the Earth's surface" |
|
3) We want to know the distance in kilometers, so 24,000 cm equals how many kilometers? Since there are 100,000 centimeters in one kilometer, you can convert 24,000 centimeters to kilometers simply by dividing by 100,000 (remember the hint?) 24,000 cm / 100,000 cm/km = 0.24 km Thus, the verbal scale would be "1 centimeter on the map = 0.24 kilometers on the Earth's surface" (again, you'll only have to do this calculation once for any given map) |
|
4) So, if 1 cm on the map = 0.24 km on the Earth's surface, then: 3 cm * 0.24 km/cm = 0.72 km |
|
Example 16 |
|
On a map, points C and D are 3.5 inches apart. How many miles is this? |
|
1) Find the ratio scale of the map. 1:24,000 |
|
2) Convert the ratio scale 1:24,000 to a verbal scale. 1 inch on the map = 24,000 inches "on the Earth's surface" |
|
3) We want to know the distance in miles, so 24,000 inches equals how many miles? There are 12 inches in 1 foot, first divide 24,000 by 12. 24,000 inches / 12 inches/foot = 2,000 feet There are 5,280 feet in one mile, so then divide the 2,000 feet by 5,280 feet. 2,000 feet / 5,280 feet/mile = 0.379 miles Thus, the verbal scale would be "1 inch on the map = 0.379 miles on the Earth's surface" |
|
4) So, if 1 inch on the map = 0.379 miles on the Earth's surface, then: 3.5 inches * 0.379 miles/inch = 1.33 miles |
![]()
![]()
Finding Places
Using Latitude and Longitude
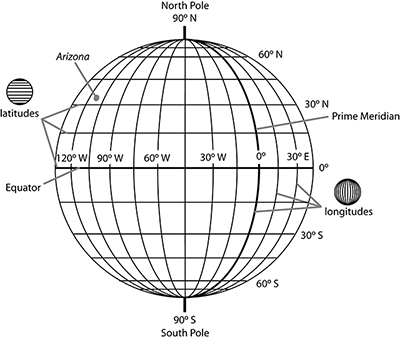
There are several geographical coordinate systems that can be used to locate features on the Earth's surface. One of the most commonly used methods can precisely locate points of interest using a grid system based on lines of latitude and longitude (see Figure 2-18).
LATITUDE - Lines of latitude trend east-west and are parallel to the Equator. Latitude measures distance north or south from the Equator, where the equator is 0° latitude and the poles are 90°. All latitudes north of the Equator are part of the northern hemisphere (0-90° north latitude), and those to the south of the Equator are part of the southern hemisphere (0-90° south latitude). Arizona is located in the northern hemisphere.
LONGITUDE - Lines of longitude trend north-south and measure distance east or west from the Prime meridian (0° longitude). All longitudes east of the Prime Meridian are part of the eastern hemisphere (0-180° east longitude), and those to the west of the Prime Meridian are part of the western hemisphere (0-180° west longitude). Arizona (and the rest of North America) is located in the western hemisphere.
Latitude and longitude coordinates on topographic maps and global positioning system (GPS) devices have different formats, including decimal degrees, degrees and decimal minutes, or degrees, minutes, and seconds (DMS). 1 degree (°) = 60 minutes ('). 1 minute (') = 60 seconds (").
|
|
|
Figure 2-18. The latitude and longitude coordinate system. |
Example 17 describes how to find the latitude and longitude of a known location on a topo map.
|
Example 17 |
|
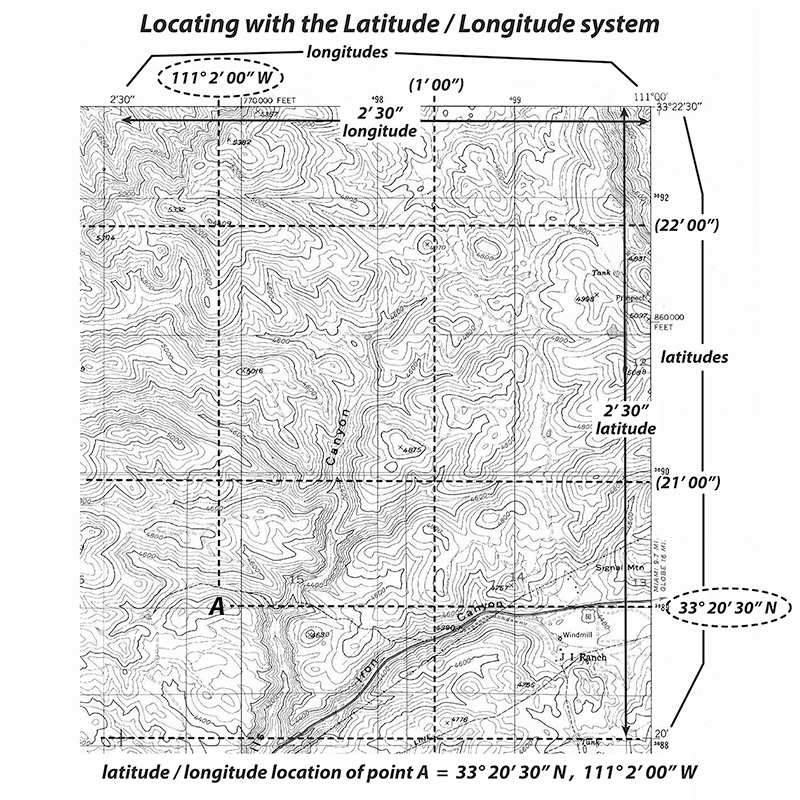
Determine the latitude and longitude of a known map location: point A. |
|
|
|
1) Latitude - Extend a line (visually or physically with a straightedge) horizontally from the location (point A) to the nearest SIDE of the map. Estimate its latitude between the nearest two coordinates. 33° 20' 30" N |
|
2) Longitude - Extend a vertical line from the location (point A) to the TOP or BOTTOM of the map. Estimate its longitude value between the nearest two coordinates. 111° 2' 0" W |
Example 18 describes how to find a location on a topo map using latitude and longitude coordinates.
|
Example 18 |
|
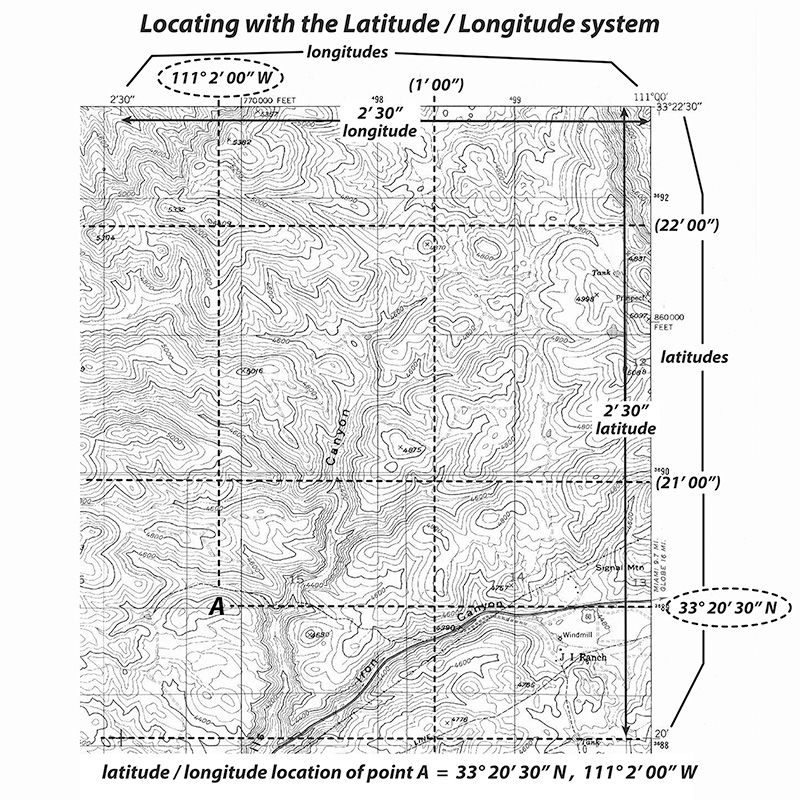
Find a location using latitude and longitude coordinates: 33° 20' 30" N, 111° 2' 0" W. |
|
|
|
1) Find the latitude value 33° 20' 30" N on the left or right side of the map. |
|
2) Extend a line horizontally from the latitude value. The location of interest is somewhere on this line. |
|
3) Find the longitude value 111° 2' 0" W on either the top or bottom of the map. |
|
4) Extend a line vertically from the longitude value. |
|
5) The location of interest is where the latitude and longitude lines intersect. point A |
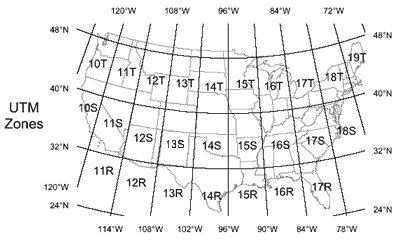
Using Universal Transverse Mercator
The Universal Transverse Mercator (UTM) coordinate system is another grid-based location method that is becoming more commonly used with the proliferation of mobile global position system (GPS) devices. UTM grid coordinates are given in units of distance (meters) that can be easily read on most topo maps. On topographic maps, northing (latitude) UTM values are listed on the side margins and represent the distance in meters from the Equator, whereas the easting (longitude) UTM values are listed along the top and bottom margins and represent the distance in meters from the zone's central meridian (see Figure 2-19).
|
|
|
Figure 2-19. The UTM coordinate system. |
Example 19 describes how to find the UTM northing (latitude) and easting (longitude) values of a known location on a topo map.
|
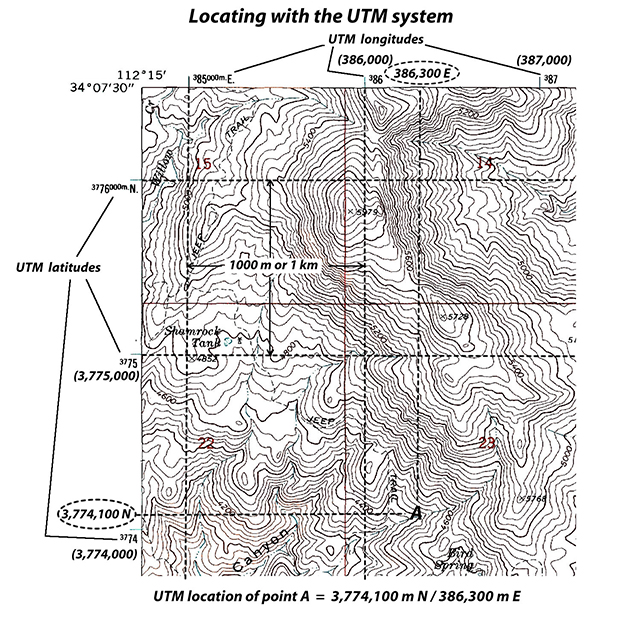
Example 19 |
|
Determine the UTM northing (latitude) and easting (longitude) values of a known map location: point A. |
|
|
|
1) Northing (latitude) - Extend a line (visually or with a straightedge) horizontally from the location (point A) to the nearest SIDE of the map, and estimate its northing value between the nearest two UTM values. 3,774,100 m N |
|
2) Easting (longitude) - Extend a line vertically from the location (point A) to the TOP or BOTTOM of the map, and estimate its easting value between the nearest two UTM coordinates. 386,300 m E |
Example 20 describes how to find a location on a topo map using UTM northing (latitude) and easting (longitude) coordinates.
|
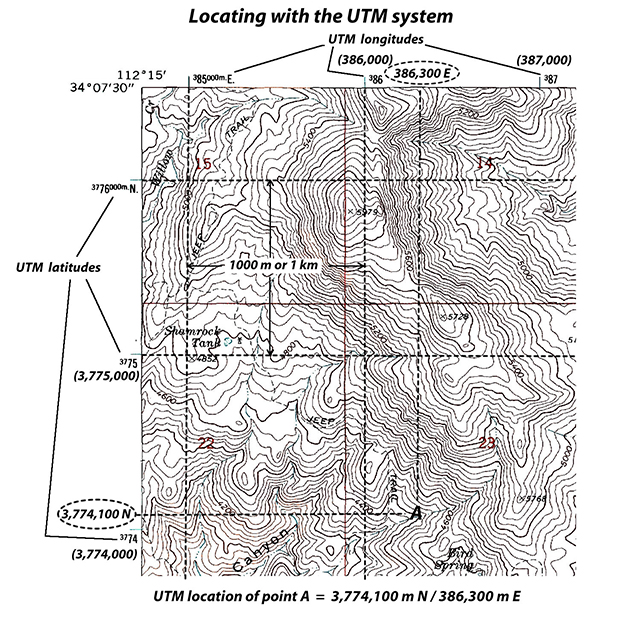
Example 20 |
|
Find a location using UTM northing (latitude) and easting (longitude) coordinates: 3,774,100 m N / 386,300 m E |
|
|
|
1) Find the northing value 3,774,100 m N on the left or right SIDE of the map. Extend a line horizontally from the northing value. The location of interest is on this line. |
|
2) Find the easting value 386,300 m E on either the TOP or BOTTOM of the map. Extend a line vertically from the easting value The location of interest is where the northing and easting lines intersect. point A |