Part A
Reading Landscapes
As shown in Figure 2-2, there are many forms of media that we can use to interpret the surface of the Earth, and you will become familiar with several of them in this lab activity. We will start with topographic maps, as they are a fundamental tool to use and understand for anyone that studies geology in the field.
Figure 2-2. Different representations of the same landscapes.
Topographic Maps
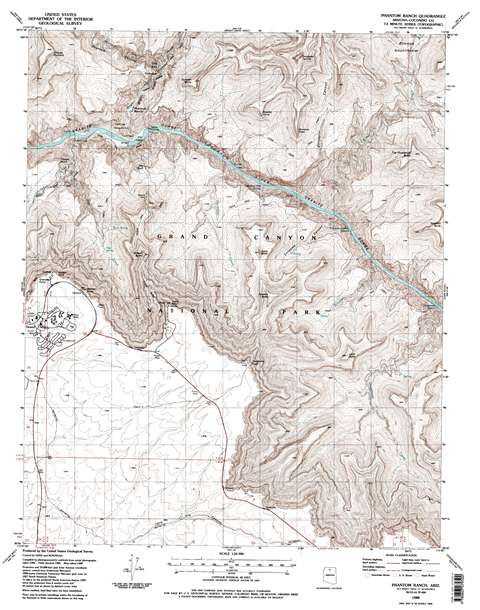
Topographic maps (a.k.a. topo maps) are a fundamental tool used by anyone who studies geology in the field. You can use the word "topography" in describing the surface features of a region (like the sea floor or the Earth's land surface), a place (a golf course fairway or a park), an object (a mineral crystal or your skin), or even a field of study (the topography of the U.S. economy). In the geographic sense, a topographic map is a two-dimensional (2-D) graphical representation of the real, three-dimensional (3-D) landscape of the Earth's surface. Figure 2-3 below is the Phantom Ranch 7.5 Minute topographic quadrangle. A topographic map is commonly referred to as a quadrangle because it is usually rectangular in shape. The "7.5 Minute" part of the map name refers to the distance between map corners in terms of minutes of latitude and longitude.
|
Figure 2-3. The Phantom Ranch 7.5 Minute Quadrangle, a topographic map that covers a portion of the Grand Canyon in Arizona. Click on the image to see a PDF of the map. |
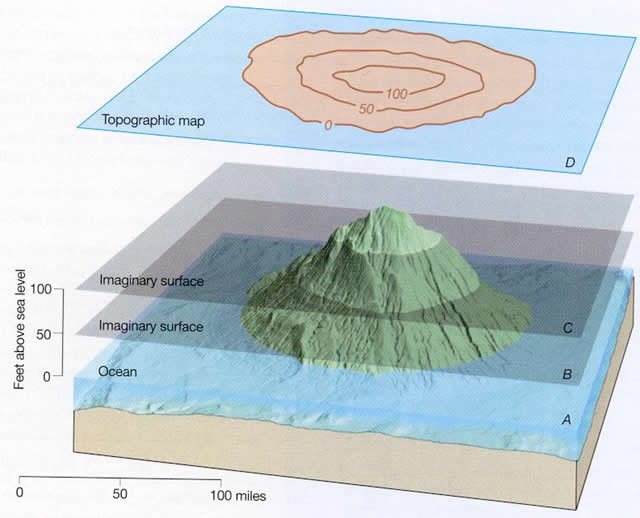
A few observations and interpretations are very helpful in guiding our ablity to read landscapes. On a topographic map, different elevations across a landscape surface are represented by various contour lines. In Figure 2-4 below, a contour line is drawn where a horizontal plane (i.e., A, B, or C) intersects the land surface. Where sea level (plane A) intersects the land, it forms the 0-foot contour line. Plane B is an imaginary surface 50 feet above sea level, so its intersection with the land forms the 50-foot contour line. Plane C is an imaginary surface 100 feet above sea level, and its intersection with the land forms the 100-foot contour line. D is the resulting topographic map of the island. It was constructed using a 50-foot contour interval (50-foot vertical increments between contour lines) above mean sea level.
|
|
|
Figure 2-4. The origin of elevation contour lines on a topographic map. |
Contour Lines
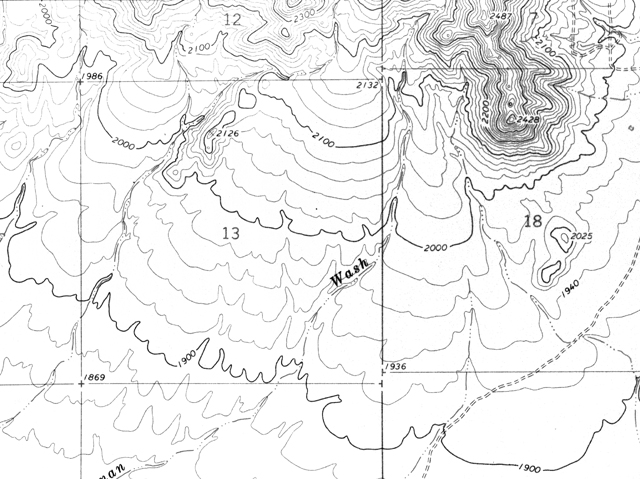
Let's discuss contour lines some more by using parts of actual topographic maps, like the one in Figure 2-5 below. The following tutorial includes answered sample questions (Examples) as well as questions that you need to answer (Quiz Me!).
|
|
|
Figure 2-5a. A portion of the New River SE 7.5 minute topographic quadrangle. |
|
|
|
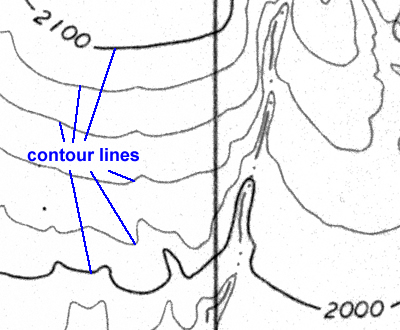
Figure 2-5b. Contour lines shown on a close-up of the New River SE 7.5 minute topographic quadrangle. |
Most of the lines on the map in Figure 2-5 are contour lines that represent different elevations. Any given contour line represents an elevation measured (in feet or meters) from some reference plane (like mean sea level). Unless otherwise stated, all topographic quadrangles used in this course have elevations measured in feet.
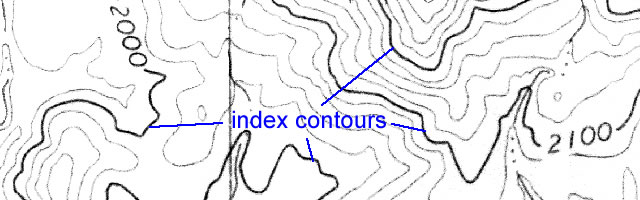
Index Contours
Note that every fifth contour line is printed darker and labeled with an elevation (see Figure 2-6). Simply follow these index contour lines until you find a number that represents its elevation. If a point lies on an index contour, its elevation can be read directly.
|
|
|
Figure 2-6. Index contour lines shown on a close-up of the New River SE 7.5 minute topographic quadrangle. |
|
Example 1 |
|
Point A lies on an index contour. What is the elevation of point A? |
|
2000 feet |
|
Example 2 |
|
Point B lies on an index contour. What is the elevation of point B? |
|
2200 feet |
![]()
![]()
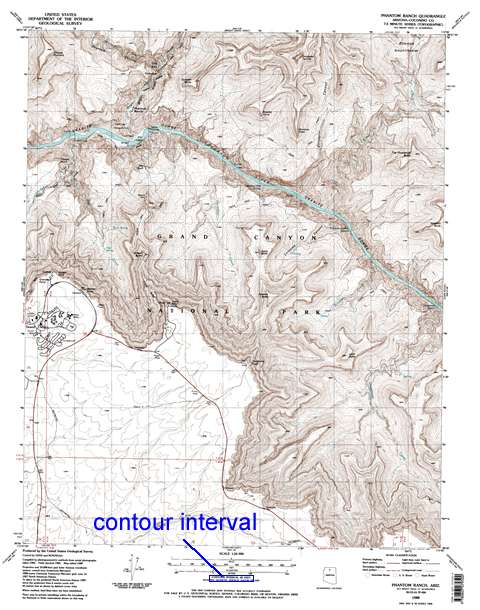
Contour Interval
The difference in elevation between any two adjacent contour lines is called the contour interval (CI) and is commonly written beneath the bar scales at the bottom of a topographic map.
|
|
|
Figure 2-7a. The location of the contour interval on the Phantom Ranch 7.5 minute quadrangle. |
|
|
|
Figure 2-7b. A close-up of the location of the contour interval on the Phantom Ranch 7.5 minute quadrangle. |
Some simple (and important) facts about contour interval:
> Values of 10 feet, 20 feet, 40 feet, and 50 feet are common contour intervals. The contour interval for the Phantom Ranch 7.5 Minute quad is 40 feet, which means that the difference in elevation between each contour line is 40 feet.
> Contour lines must be multiples of the contour interval used on the map. For example, if the contour interval is 40 feet, only numbers evenly divisible by 40 (like 40, 80, 120, 160, 200, etc.) can be used as contour lines on the map.
> The size of the contour interval depends on the amount of elevation change across a map. In flat or gently sloping areas, the contour interval is a low number (like 10 or 20 feet), whereas in very steep areas, it is a high number (like 100 feet or more).
> The contour interval can be easily calculated by finding the elevation difference between adjacent index contours and divide by the number of contours (usually 5) between index contours (including the next index contour). See Figure 2-8 below.
Figure 2-8. Determining the contour interval.
|
Example 3 |
|
What is the contour interval of this map? |
|
C.I. = 6900 feet - 6800 feet = 100 feet / 5 = 20 feet |
![]()
![]()
More About Determining Elevations
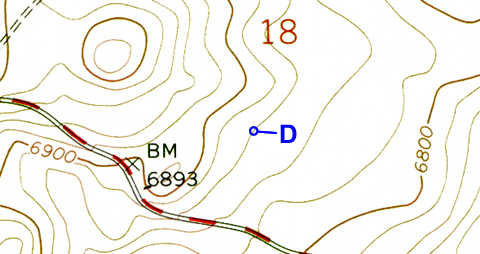
Notice that most contour lines are not labeled with any elevation number. The elevation of any contour can be found by counting the number of contour lines (and thus contour intervals) up or down from the nearest index contour line. Be sure to count using the contour interval given for the map.
|
|
|
Figure 2-9. A point located on an unlabeled contour line. Point D is located 3 contours above the 6800-foot contour, so its elevation is 6800 + 20 + 20 + 20 = 6860 feet. Alternatively, point D is located 2 contour lines below the 6900-foot contour, so its elevation is 6900 - 20 - 20 = 6860 feet. |
|
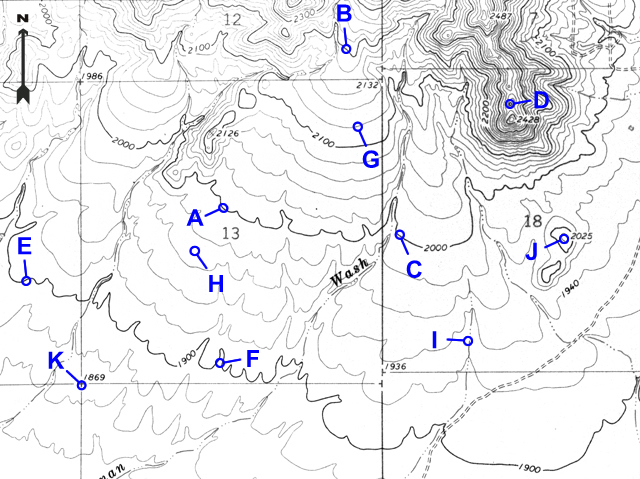
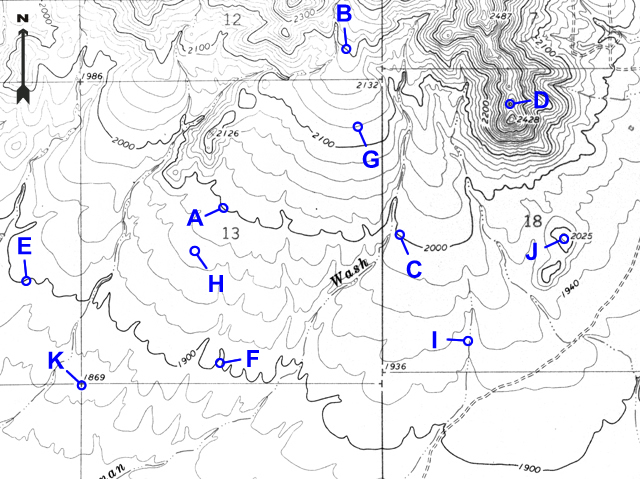
Example 4 |
|
What is the elevation of point G? |
|
2100 feet + one 20-foot CI = 2120 feet |
![]()
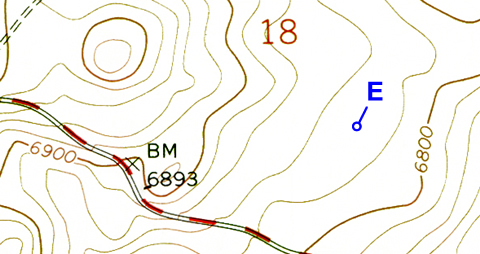
When a point lies between contour lines, its elevation must be estimated by judging distance from the nearest contour lines.
|
|
|
Figure 2-10. A point located between contour lines. Point E is located about halfway between the 6820-foot contour and the 6840-foot contour, so its elevation is 6830 feet. |
|
Example 5 |
|
What is the elevation of point H? |
|
About halfway between the 1980-foot and 1960-foot contours, so 1970 feet |
![]()
![]()
![]()
![]()
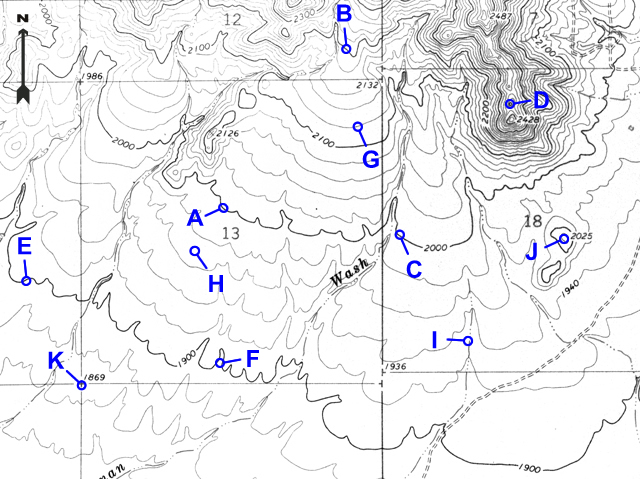
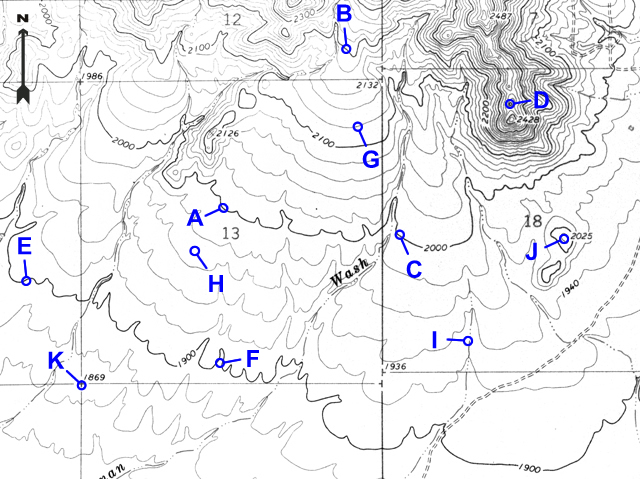
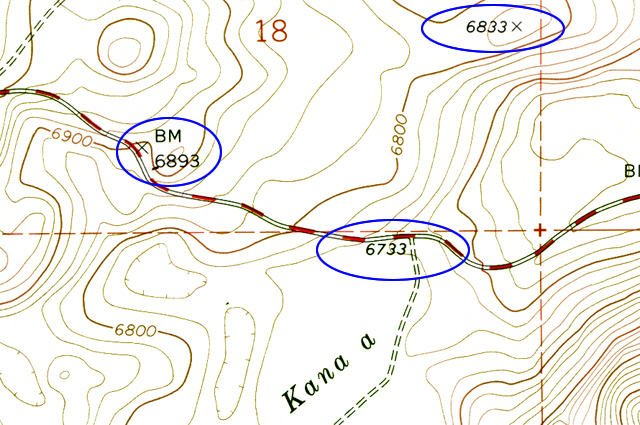
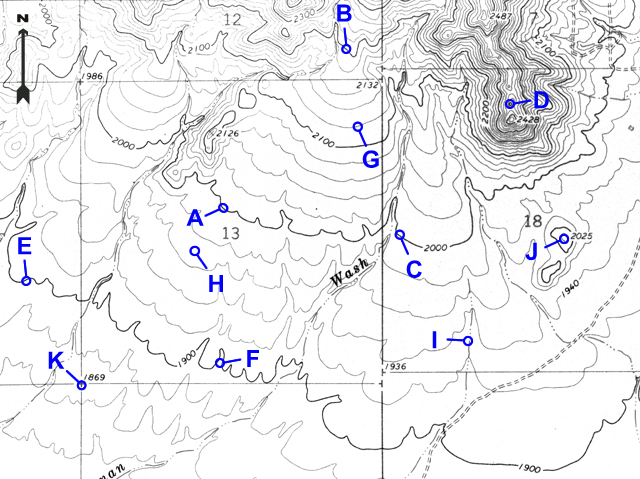
Many points are marked with number elevations. These "spot elevations" have either a number elevation or an "X" and the number elevation. Locations having other symbols or "BM" (benchmarks) are places where elevations have been more precisely surveyed.
|
|
|
Figure 2-11. Spot elevations and benchmarks. The location marked by "X" and labeled "BM 6893" is a benchmark. The "6833" is a spot elevation for the location marked by the "X" on that hill top. The "6733" is a spot elevation for the road intersection. |
|
Example 6 |
|
What is the elevation of the hill top at point J? |
|
2025 feet |
|
Example 7 |
|
What is the elevation of the section corner at point K? |
|
1869 feet |
![]()
![]()
Any given contour line (whether it's an index contour or a normal one) connects points of equal elevation. This means that every point on that contour line has the same elevation. A contour line represents only one elevation, so movement across a contour line represents uphill or downhill movement. In this way, contour lines separate areas of lower elevation from areas of higher elevation.
![]()
Interpreting Contour Shape and Spacing
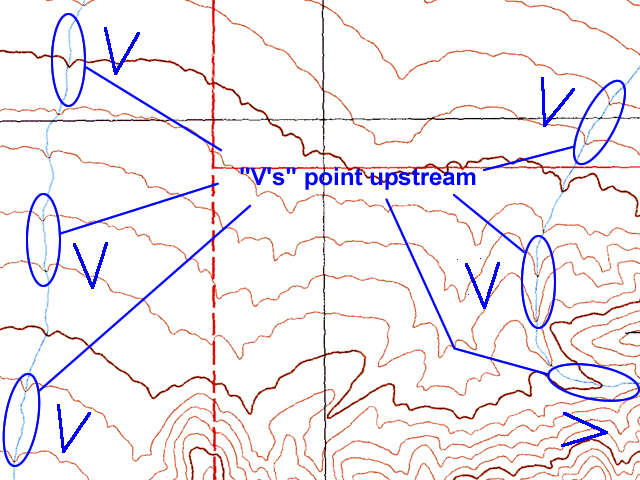
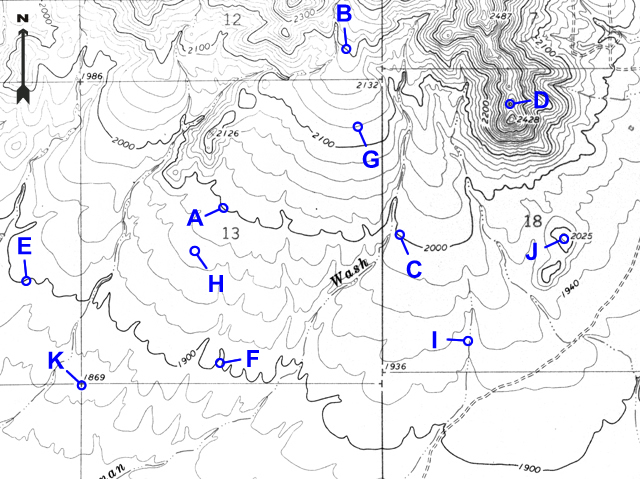
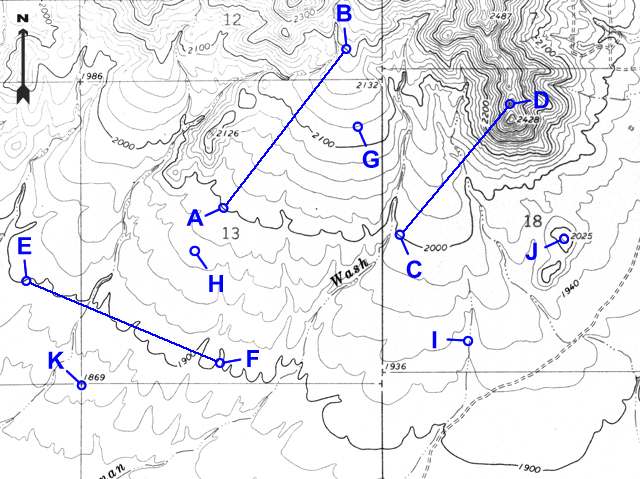
When contour lines cross a stream, the contours bend, or form V-shaped patterns. The "V" always points upstream (or uphill) and can be used to determine the flow direction for the stream.
|
|
|
Figure 2-12. The "Rule of the V's" is an easy way to determine the direction of stream drainage. |
|
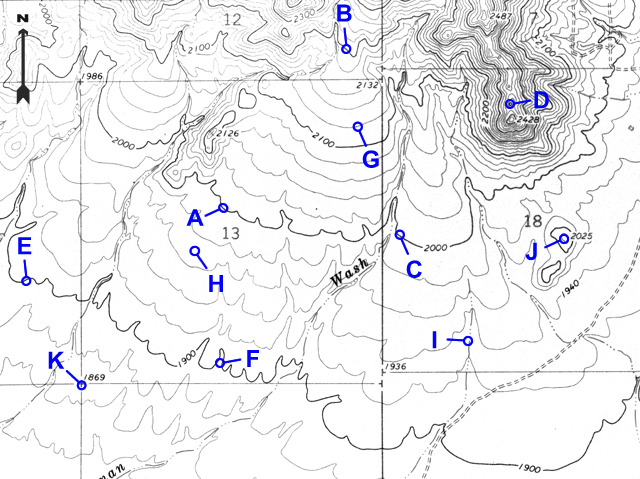
Example 8 |
|
Which way does the stream flow at point I? |
|
South (the vees point upstream/north) |
![]()
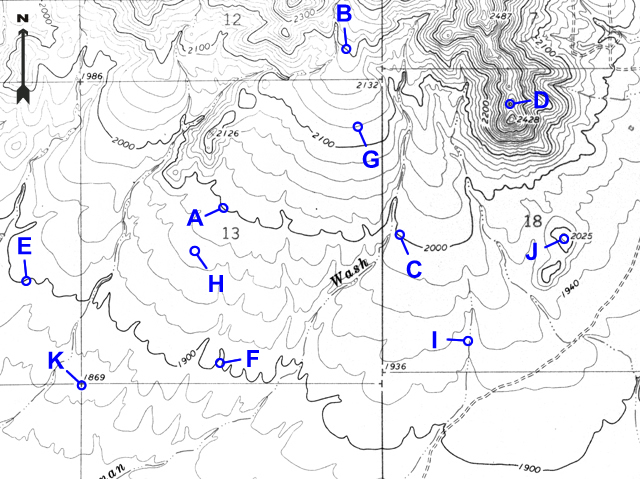
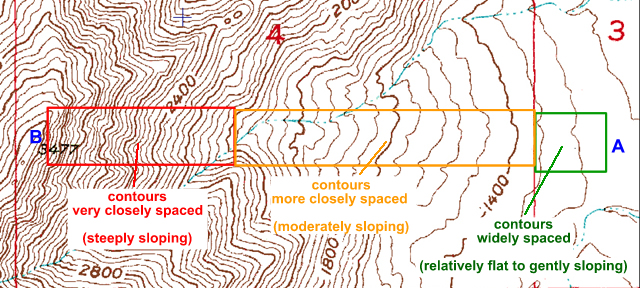
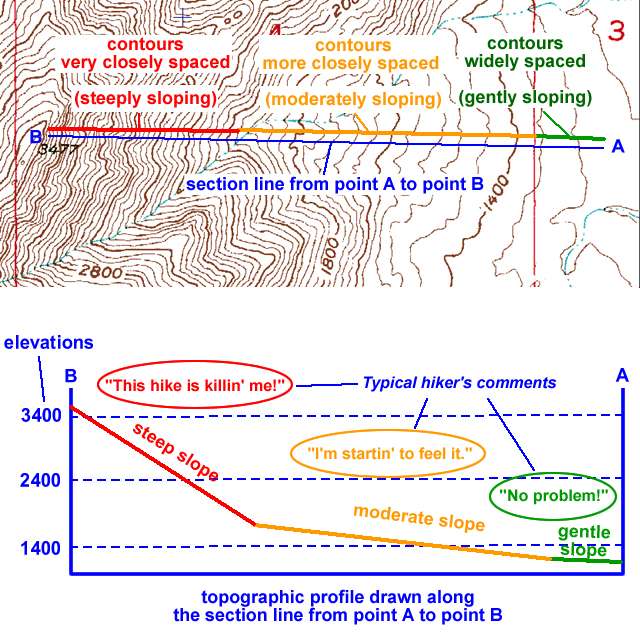
Contour lines make many patterns, but never cross or split. The degree of slope can be inferred from the relative spacing of contour lines: widely spaced contour lines represent a gentler slope, whereas closely spaced contours indicate steep slopes.
|
|
|
Figure 2-13. The degree of slope can be determined by the relative spacing of contour lines in an area. |
|
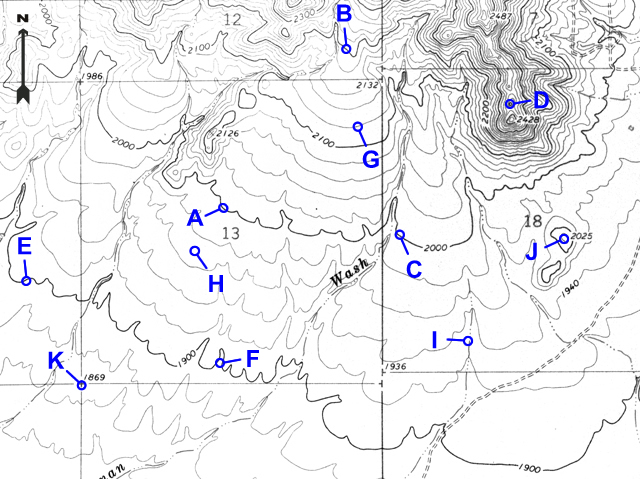
Example 9 |
|
At which point is the slope the steepest: A, C, D, or F? |
|
D |
|
Example 10 |
|
At which point is the slope the most flat: B, G, or E? |
|
E |
![]()
![]()
![]()
Topographic Profiles
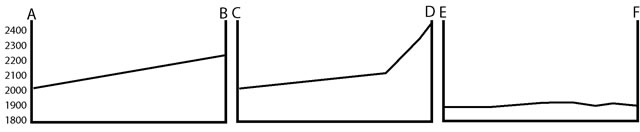
A topographic profile shows elevation changes along a certain line (a section line) and shows the slope of the land surface from the side.
|
|
|
Figure 2-14. A topographic profile shows the changes in the slope of the ground surface from one point to another. |
|
Example 11 |
|
Which topographic profile shows mostly a gentle slope with a steep slope at one end? |
|
C-D |
|
Example 12 |
|
Which topographic profile line has little or no elevation change? |
|
E-F |
![]()
![]()
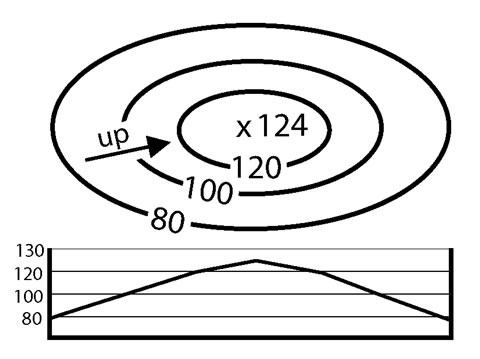
Hills and ridges are represented by closed, commonly concentric contours. The more contour lines on hill or ridge, the higher it is.
|
|
|
Figure 2-15. A simplified map showing contour lines that represent a hill. The corresponding topographic profile for hill is also shown. |
![]()
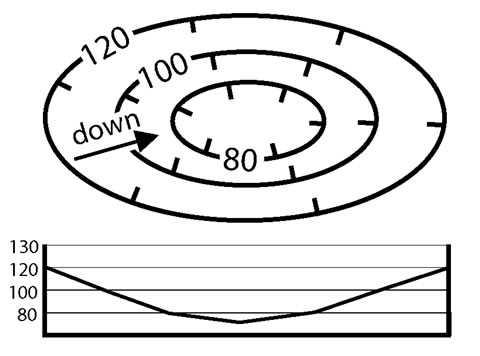
Basins or depressions (low areas having no drainage outlet) in the landscape are shown by closed contours with short lines (hachures) that point downhill. The depth of the depression can be estimated in the same way as we do for hills: by taking the difference in elevation between high and low points.
|
|
|
Figure 2-16. A simplified map showing contour lines that represent a basin. The corresponding topographic profile for basin is also shown. |
![]()