Part C
Estimating Crater Depth
A simple, but useful relationship can be used to determine the depth of craates and the height of mountain peaks. How can we determine the depth of some craters from far above a planet's surface? One technique involves simple trigonometry (the study of triangles).
|
|
|
Figure 8-4. The eastern edge of Mare Imbrium. Craters and peaks: A = Aristillus, B = Autolycus, C = Archimedes, D = Theaetetus, and G = Cassini. Peaks: E = Mons Piton and F = Montes Spitzbergen. |
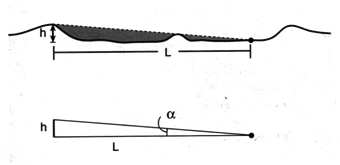
A crater's depth can be determined if the following are known: 1) the length of the shadow cast by the crater rim and 2) the angle of incoming light, as shown in Figure 8-5 below:
|
|
|
Figure 8-5. Estimating the crater depth using simple trigonometry. |
The following formula describes this relationship:
h = L * TANα
where h = depth of the crater, L = length of the shadow, and α = the angle of incoming light.
Use the infromation in Figures 8-4 and 8-5 to answer Quiz Me! questions C26 through C30.
![]()
![]()
![]()
![]()
![]()