The definition of average velocity is:

According to this definition, the vector average velocity is obtained by dividing a vector by a scalar. Since the scalar () is always positive, this definition indicates that the two vectors ( and ) have the same direction. The diagrams below illustrate this idea graphically for a ball that is rolling along a straight track.

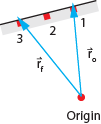Suppose that a ball rolls from point 1 to 2 to 3 along the track in the diagram at right. In addition, suppose that we would like to determine the direction of the velocity of the ball when it is at position 2. Recall that a position vector is a vector from the origin to the location of an object. The diagram shows the position of a ball at two different instants: just before and just after the ball passes point 2. The location of the origin in this diagram is arbitrary. Its location will not affect the direction of the velocity that we are computing.

Recall that displacement is the difference between the final and initial position:

.

This is equivalent to saying that the displacement is the quantity that must be added to the initial position in order to obtain the final position:

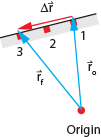The red vector in the diagram at right is arranged head-to-tail with the initial position vector. Hence, graphically, they are being added. Together, they start at the origin and end at point 3, just as the final position vector does. Hence, the red vector must be the displacement vector. As you can see, the displacement vector goes from the initial to final location of the rolling ball.

The definition for average velocity states:

Since is positive, the directions of the average velocity and the displacement vectors must be the same. At the moment, we are concerned with the velocity's direction, not its magnitude. Hence, the vectors diagrammed above are only intended to show their directions, not their relative magnitudes.

If the interval is short enough, then the average velocity for the interval is equal to the instantaneous velocity at the midpoint of the interval, point 2. This is illustrated in the diagram at right. Notice that the resulting velocity vector is tangent to the track (i.e., the trajectory of the ball rolling along the track).

In summary, the velocity of the ball as it passes a given point on the track is tangent to the track at that location.