The definition of average acceleration is:

According to this definition, the vector average acceleration is obtained by dividing a vector by a scalar. Since the scalar () is always positive, this definition indicates that the two vectors ( and ) have the same direction. We would like to apply this definition to find the direction of the acceleration at point D. Then and in the definition correspond to an interval that spans point D, i.e., an interval with an initial point just before point D and with a final point just after point D. The diagrams below illustrate this idea graphically.

 

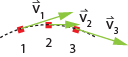Suppose that a ball follows a parabolic trajectory. It goes upward from point 1 to 2, then downward from point 2 to 3. Point 2 is at the apex of the parabola so the speed at point 2 is the slowest. Hence the length of is the shortest. Assume that point 2 is at the exact center of the interval from point 1 to 3. Then the speeds at point 1 and 3 are equal.

 

Recall that the change in velocity between the final point (point 3) and the initial point (point 1) is:

.

This is equivalent to saying that is the quantity that must be added to the initial velocity in order to obtain the final velocity:

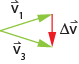The diagram at right shows the vector (the red vector) that must be graphically added to vector to obtain . Hence, the red vector must be .

 

According to the definition of average acceleration,

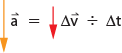
Since is a positive scalar, the direction of the acceleration must be the same as the direction of the change in velocity. The relative magnitudes of and depend on the value of .

 

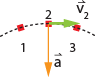If the interval is short enough, then the average acceleration for the interval is equal to the instantaneous acceleration at the midpoint of the interval, point 2. This is illustrated in the diagram at right. Notice that the resulting acceleration vector is perpendicular to the velocity at point 2.

 

In summary, the acceleration will be perpendicular to the velocity whenever an object turns but is not speeding up or slowing down. In addition, the acceleration is directed toward the interior of the turn.

 

Having demonstrated the theory above, recall that the acceleration for an object that is flying through a vacuum is the freefall acceleration (i.e., the acceleration of gravity). The freefall acceleration has a magnitude of 9.8m/s² and is directed vertically downward.